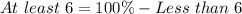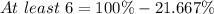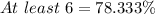Answer:
(a) See attachment for table
(b)
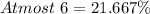
(c)
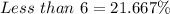
(d)
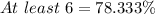
Explanation:
Given
The data (in the question)
Solving (a): Frequency and Relative frequencies of each data
The range of the data is 0 to 8. So the frequency of each is the number of times each of 0 - 8 occurs.
This is tabulated below:

The relative frequency is calculated as:
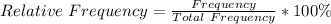
For instance: When x = 0:
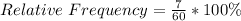
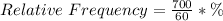
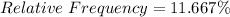
Solving (b): Proportion that have at most 6.
Here, we consider frequencies of 0 to 6.
This is represented as thus:

Add up the relative frequencies to get the proportion
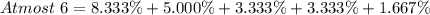
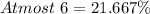
Solving (c): Proportion that have at fewer than 6.
Here, we consider frequencies of 0 to 5.
This is represented as thus:

Add up the relative frequencies to get the proportion
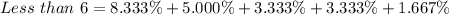
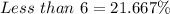
Solving (d): Proportion that have at least 6.
Here, we make use of the complement rule: