Given:
The bases of triangular prism are right triangles with a base of 12 inches and height of 9 inches.
The height of the prism is 11 inches.
To find:
The surface area of the triangular prism.
Solution:
Using the Pythagoras theorem, the hypotenuse of the bases of the triangular prism is:
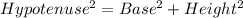
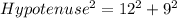
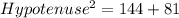
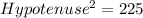
Taking square root on both sides.
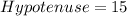
The surface after of the triangular prism contains 3 rectangles of dimensions 12 inches by 11 inches, 9 inches by 11 inches, 15 inches by 11 inches and two triangles with base 12 inches and height 9 inches.
Area of the rectangle:
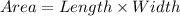
So, the area of three rectangles are:
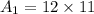

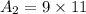
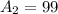
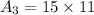
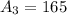
Area of a triangle is:
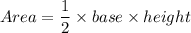
So, the area of the triangles is:
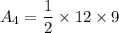
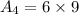
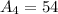
And, the triangles have same dimensions so their areas are equal.
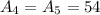
Now,
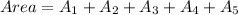
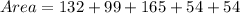
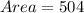
Therefore, the surface area of the triangular prism is 504 sq. inches.