Question

A railroad car moving at a speed of 3.46 m/s overtakes, collides and couples with two coupled railroad cars moving in the same direction at 1.40 m/s. All cars have a mass of mass 1.6 104 kg. Determine the following.(a) speed of the three coupled cars after the collision (Give your answer to at least 2 decimal places.) m/s(b) kinetic energy lost in the collision J

Answer 1

`2.09\ \text{m/s}`

`22298.4\ \text{J}`

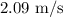
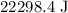
Step-by-step explanation:

m = Mass of each the cars =
`1.6* 10^4\ \text{kg}`

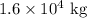
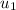`u_1` = Initial velocity of first car = 3.46 m/s

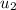`u_2` = Initial velocity of the other two cars = 1.4 m/s

v = Velocity of combined mass

As the momentum is conserved in the system we have

`mu_1+2mu_2=3mv\\\Rightarrow v=(u_1+2u_2)/(3)\\\Rightarrow v=(3.46+2* 1.4)/(3)\\\Rightarrow v=2.09\ \text{m/s}`

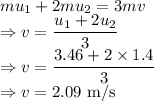
Speed of the three coupled cars after the collision is
`2.09\ \text{m/s}`.

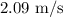As energy in the system is conserved we have

`K=(1)/(2)mu_1^2+(1)/(2)2mu_2^2-(1)/(2)3mv^2\\\Rightarrow K=(1)/(2)* 1.6* 10^4* 3.46^2+(1)/(2)* 2* 1.6* 10^4* 1.4^2-(1)/(2)* 3* 1.6* 10^4* 2.09^2\\\Rightarrow K=22298.4\ \text{J}`

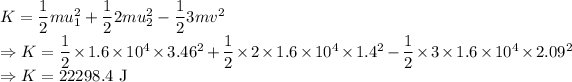
The kinetic energy lost during the collision is
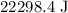`22298.4\ \text{J}`.