Answer:
AC = 4.5 units
Explanation:
Given question is incomplete without the figure; find the figure attached.
By applying angle bisector theorem in the given triangle ABC,
(Since, AD is the angle bisector of ∠BAC)

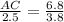
AC =
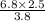
AC = 4.47
AC ≈ 4.5 units
Length of side AC in the given triangle = 4.5 units.