Answer:
The doomsday is 146 days
Explanation:
Given
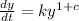
First, we calculate the solution that satisfies the initial solution
Multiply both sides by
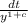
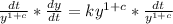
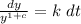
Take integral of both sides
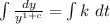
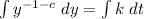
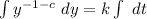
Integrate
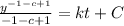
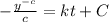
To find c; let t= 0
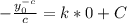
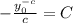
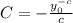
Substitute
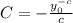 in
in
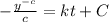
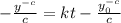
Multiply through by -c
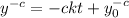
Take exponents of
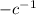
![y^{-c*-c^(-1)} = [-ckt+y_0^(-c)]^{-c^(-1)](https://img.qammunity.org/2022/formulas/mathematics/college/3nj4jnjexf6zzll3lalt8op2tv840fjpu9.png)
![y = [-ckt+y_0^(-c)]^{-c^(-1)](https://img.qammunity.org/2022/formulas/mathematics/college/ff0ijdpa4dvzxid9txih4ymavkeldar59t.png)
![y = [-ckt+y_0^(-c)]^{-(1)/(c)}](https://img.qammunity.org/2022/formulas/mathematics/college/gdxy8n5c3l01rtknhgqdv9mf85kgk0pb3c.png)
i.e.
![y(t) = [-ckt+y_0^(-c)]^{-(1)/(c)}](https://img.qammunity.org/2022/formulas/mathematics/college/4p6s7099hfxcflxzaal36czr3bevwj9knn.png)
Next:
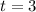 i.e. 3 months
i.e. 3 months
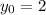 --- initial number of breeds
--- initial number of breeds
So, we have:
![y(3) = [-ck * 3+2^(-c)]^{-(1)/(c)}](https://img.qammunity.org/2022/formulas/mathematics/college/1866ua033w56o17dieiyr48rq0nz832n2e.png)
-----------------------------------------------------------------------------
We have the growth term to be:
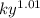
This implies that:
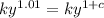
By comparison:
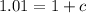
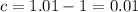
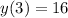 --- 16 rabbits after 3 months:
--- 16 rabbits after 3 months:
-----------------------------------------------------------------------------
![y(3) = [-ck * 3+2^(-c)]^{-(1)/(c)}](https://img.qammunity.org/2022/formulas/mathematics/college/1866ua033w56o17dieiyr48rq0nz832n2e.png)
![16 = [-0.01 * 3 * k + 2^(-0.01)]^{(-1)/(0.01)}](https://img.qammunity.org/2022/formulas/mathematics/college/tfn7p0gbtej2mju3aktcdzu7ltcgpi2120.png)
![16 = [-0.03 * k + 2^(-0.01)]^(-100)](https://img.qammunity.org/2022/formulas/mathematics/college/2ft9txe7zyhy9ccc7ysylloznayjs7jarr.png)
![16 = [-0.03 k + 0.9931]^(-100)](https://img.qammunity.org/2022/formulas/mathematics/college/j4mmximwznuyskfye5wr60ayryoiq35qeg.png)
Take -1/100th root of both sides
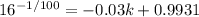
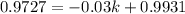
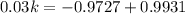
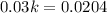
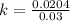
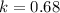
Recall that:
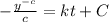
This implies that:
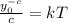
Make T the subject
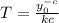
Substitute:
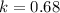 ,
,
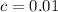 and
and
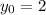
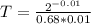
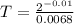
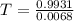
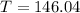
The doomsday is 146 days