Question

The population of rabbits on an island is growing exponentially. In the year 1995, the population of rabbits was 1000, and by 1999 the population had grown to 1800. Predict the population of rabbits in the year 2003, to the nearest whole number.

Answer 1

Given:

The population of rabbits on an island is growing exponentially.

In the year 1995, the population of rabbits was 1000, and by 1999 the population had grown to 1800.

To find:

Expected population of rabbits in the year 2003, to the nearest whole number.

Solution:

The exponential growth model is:

`y=ab^t`

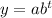
Where, a is the initial value, b is the growth factor, t is the number of years.

Let y be the population of rabbits t years after 1995.

In the year 1995, the population of rabbits was 1000, it can be written as (0,1000) and by 1999 the population had grown to 1800, it can be written as (4,1800).

For (0,1000),

`1000=ab^0`

`1000=a(1)`

`1000=a`

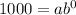
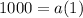
For (4,1800) and a=1000, we get

`1800=1000b^4`

`(1800)/(1000)=b^4`

`1.8=b^4`

`(1.8)^{(1)/(4)}=b`

`b\approx 1.1583`

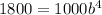
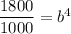
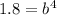
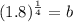
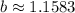
The required exponential model is:

`y=1000(1.1583)^t` ...(i)

in year 2003, the number of years since 1995 is 8.

Putting t=8 in (i), we get

`y=1000(1.1583)^8`

`y=3240.1748`

`y\approx 3240`

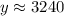
Therefore, the population of rabbits in the year 2003 is 3240.

Answer 2

3,240

Explanation:

The computation of the population of rabbits in the year 2003 is shown below:

Given that

In the year 1995, the population of the rabbits was 1000

And, in 1999 the population of the rabbits grown to 1,800

So there is an increase of

= (1800 - 1000) ÷ 1000

= 80%

So for 2003, the population of the rabbits is

= 1800 + (1800 × 0.80)

= 3,240