Answer:
interest point:
1) Point on the left side
2) Point within the radius r₁ of the first sphere
3) Point between the two spheres
4) point within the radius r₂ of the second sphere
5) Right side point
Step-by-step explanation:
In this case, the total electric field is the vector sum of the electric fields of each sphere, to simplify the calculation on the line that joins the two spheres
We will call the sphere on the left 1 and it has a positive charge Q with radius r1, the sphere on the right is called 2 with charge -Q with radius r2. The total field is
E_ {total} = E₁ + E₂
E_{ total} =
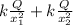
the bold indicate vectors, where x₁ and x₂ are the distances from the center of each sphere. If the distance that separates the two spheres is d
x₂ = x₁ -d
E total =
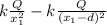
Let's analyze the field for various points of interest.
1) Point on the left side
in this case
E_ {total} =
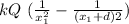
E_ {total} =
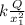
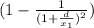
We have several interesting possibilities:
* We can see that as the point is further away the field is more similar to the field created by two point charges
* there is a point where the field is zero
E_ {total} = 0
x₁² = (x₁ + d)²
2) Point within the radius r₁ of the first sphere.
In this case, according to Gauus' law, the charge is on the surface of the sphere at the point, there is no charge inside so this sphere has no electric field on its inner point
E_ {total} =
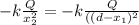
this expression holds for the points located at
-r₁ <x₁ <r₁
3) Point between the two spheres
E_ {total} =
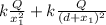
This champ is always different from zero
4) point within the radius r₂ of the second sphere, as there is no charge inside, only the first sphere contributes
E_ {total} =
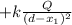 + k Q / (d-x1) 2
+ k Q / (d-x1) 2
point range
-r₂ <x₂ <r₂
5) Right side point
E_ {total} =
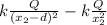
E_ {total} =
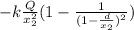 - k Q / x22 (1- 1 / (x1 + d) 2)
- k Q / x22 (1- 1 / (x1 + d) 2)
we have two possibilities
* as the distance increases the field looks more like the field created by two point charges
* there is a point where the field is zero