Answer:

Explanation:
In a parallelogram, opposite angles are congruent, so they have the same measure by the definition of congruence. Therefore,
 , so
, so
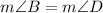 . We are given the measures of these two angles, so we can write the following equation to solve for
. We are given the measures of these two angles, so we can write the following equation to solve for
 :
:

Solving for
 , we get:
, we get:

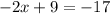 (Subtract
(Subtract
 from both sides of the equation)
from both sides of the equation)
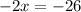 (Subtract
(Subtract
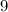 from both sides of the equation to isolate
from both sides of the equation to isolate
 )
)
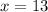 (Divide both sides of the equation to get rid of
(Divide both sides of the equation to get rid of
 's coefficient)
's coefficient)
Therefore,
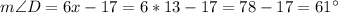 .
.
Hope this helps!