Question

A. Y = 1/3(3)^x
B. Y= 3(1/3)^x
C. Y= (1/2)^x +2
D. Y=(2)^x - 1

Answer 1

B

Explanation:

Look at the graph, it passes to (0,3), so you need to replace that coordinate into A,B,C,D. Then you can see, there is only B and C satisfies.

`Y=3((1)/(3) )^(0)=3.1=3.`

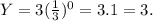
and

`Y=((1)/(2) )^(0)+2=1+2=3`

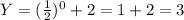
Next step, you can see when x approach to infinite then Y approach to 0.

Hence, we will take limit of B and C, if limit B or C equals to 0 then we will choose.

`\lim_(x \to \infty) {3((1)/(3))^x=3. \lim_(x \to \infty) {((1)/(3))^x=3.0=0`

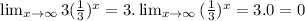
and

`\lim_(x \to \infty) {[((1)/(2))^x+2]}= \lim_(x \to \infty) {((1)/(2))^x}+ \lim_(x \to \infty) {2}=0+2=2`

We can see that only B is satisfied.