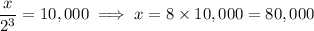Question

half life, for my physics but pretty sure it involves maths. you don’t have to do them all i’m just confused how to work it out.

Answer 1

I probably don't have to tell you that the other answer is nonsense, but I'll do it all the same, just in case... Half-life is defined as the time it takes for some radioactive substance to decay to half its original amount.

If it takes n half-lives for some substance with a starting amount of A to decay to a final amount of B, then

`B = (A)/(2^n)`

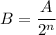
1. If the half-life is x, then after 1 half-life, 5000 units of this substance decays to 2500 units. After another half-life, this decays to 1250. After another, this in turn decays to 625.

So 3 half-lives are required.

In terms of the equation above, we solve for n such that

`625 = (5000)/(2^n) \implies 2^n = 8 \implies n=3`

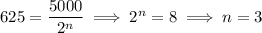
since 2³ = 8.

2. Count how many times you halve 15,000 to end up with 3750:

15,000/2 = 7500

7500/2 = 3750

===> 2 half-lives

In other words,

`3750 = (15,000)/(2^n) \implies 2^n = 4 \implies n=2`

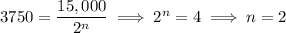
3. After 1 half-life, you would end up with

12,000/2 = 6000

and after another half-life,

6000/2 = 3000

i.e.

`(12,000)/(2^2) = \frac{12,000}4 = 3000`

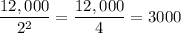
4. After 1 half-life, you have

26,000/2 = 13,000

After 2 half-lives,

13,000/2 = 6500

After 3 half-lives,

6500/2 = 3250

After 4 half-lives,

3250/2 = 1625

i.e.

`(26,000)/(2^4) = (26,000)/(16) = 1625`

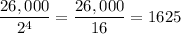
5. If the half-life is 3 years, then 15 years = 3 half-lives.

In the last 3 years, 20,000 would have decayed to 10,000.

In the second-to-last 3 years, 40,000 would have decayed to 20,000.

In the first 3 years, 80,000 would have decayed to 40,000.

i.e.

`(x)/(2^3) = 10,000 \implies x = 8*10,000 = 80,000`