HELP ME PLZZZZZZZZZZZZZZ

Question

asked Nov 8, 2022 4.3k views

1 Answer

Ugurcan Yildirim · Answer 1 · 2022-11-14T09:53:59+0000

Given:

The quadratic equation is

y=3x^2-18x+15

To find:

The x-coordinate and y-coordinate of the vertex.

Solution:

If a quadratic function is defined by
f(x)=ax^2+bx+c , then the vertex is defined as:

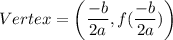
$Vertex=\left((-b)/(2a),f((-b)/(2a))\right)$

If
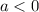a<0 , then the function has a maximum at the vertex and ff
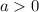a>0 , then the function has a minimum at the vertex.

We have,

y=3x^2-18x+15

Here,
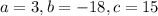a=3,b=-18,c=15 .

Since
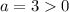, therefore the function has a minimum at the vertex. So, fill min in first blank.

Now,

(-b)/(2a)=(-(-18))/(2(3))

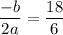
(-b)/(2a)=(18)/(6)

(-b)/(2a)=3

Putting x=3 in the given function, we get

y=3(3)^2-18(3)+15

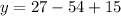
y=27-54+15

y=-12

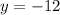
Therefore, the vertex is at point (3,-12).