Question

Find a point K on the segment with endpoints F(-8, 10) and G(8, -2) that

partitions the segment, starting at point F 3/4 of the way to point G

Answer 1

Given:

The endpoints of a line segment are F(-8, 10) and G(8, -2).

Point K partitions the segment, starting at point F
`(3)/(4)` of the way to point G.

To find:

The coordinates of point K.

Solution:

Section formula: If a point divides a line segment in m:n, then the coordinates of that point are

`Point=\left((mx_2+nx_1)/(m+n),(my_2+ny_1)/(m+n)\right)`

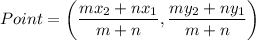
According to the given information,

`(FK)/(FG)=(3)/(4)`

`FK:FG=3:4`

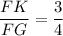
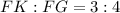
Now,

`FK:KG=FK:(FG-FK)`

`FK:KG=3:(4-3)`

`FK:KG=3:1`

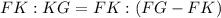
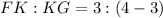
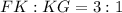
It means point K divides the segment in 3:1.

Using the section formula, we get

`K=\left((3(8)+1(-8))/(3+1),(3(-2)+1(10))/(3+1)\right)`

`K=\left((24-8)/(4),(-6+10)/(4)\right)`

`K=\left((16)/(4),(4)/(4)\right)`

`K=\left(4,1\right)`

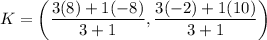
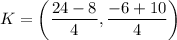
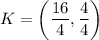
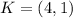
Therefore, the coordinates of the point K are (4,1).