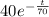Answer:
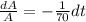
A(t) =
Explanation:
Given - A tank contains 350 liters of fluid in which 40 grams of salt is dissolved. Pure water is then pumped into the tank at a rate of 5 L/min; the well-mixed solution is pumped out at the same rate. Let the A(t) be the number of grams of salt in the tank at time t.
To find - Find the rate at which the number of grams of salt in the tank is changing at time t.
Find the number A(t) of grams of salt in the tank at time t.
Proof -
Given that,
Total fluid in the tank = 350 litres
Total salt = 40 grams
Rate in flow = 5 L/min
Rate out flow = 5 L/min
Concentration in = 0
Concentration out = (Amount of salt at time t )/ (Solution in tank at time t)
Now,
Total solution in the tank at time t = Total fluid in the tank + (Rate in flow - Rate out flow )t
= 350 + (5 - 5)t
= 350
⇒Solution in the tank at time t = 350
⇒Concentration out =
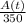
Now,
Rate of change in the tank at time t =
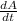
= (Rate in flow )( Concentration In) - (Rate out flow )( Concentration out)
= 5(0) - 5(
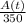 )
)
= 0 -
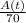
=
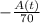
⇒
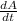 =
=
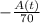
⇒
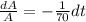
Integrate both sides , we get
ln(A) =
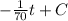
⇒A(t) =
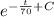
=

=
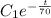
⇒A(t) =
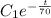
Now,
Given that,
Initially, the tank has 40 grams of salt
⇒A(0) = 40
⇒C₁ = 40
⇒A(t) =