Answer:
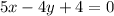
Explanation:
Given: A point which is perpendicular to the line .
To find: The equation of the line which passes through
 and is perpendicular to the line
and is perpendicular to the line
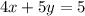 .
.
Solution:
We have,
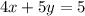 .
.
Slope of the line
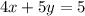 is
is
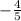 .
.
The line which passes through
 is perpendicular to the line
is perpendicular to the line
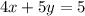 .
.
Now, the product of the slopes of two perpendicular lines is
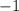 .
.
Therefore,
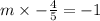
So, its slope is
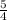 .
.
Now, the equation of the line which passes through
 and slope
and slope
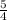 is:
is:
![y-(-4)=(5)/(4) [x-(-4)]](https://img.qammunity.org/2022/formulas/mathematics/high-school/h7ctiutw4xmd39bdbcaz6ha16ebonifimn.png)
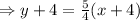
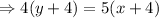
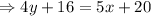
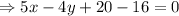
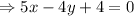
Hence, the equation of the line that contains the point
 and is perpendicular to the line
and is perpendicular to the line
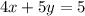 is
is
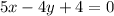 .
.