Question

The number of bacterial colonies of a certain type in samples of polluted water has a Poisson distribution with a mean of 3 per cubic centimeter (cm3). (a) If eight 1 cm3 samples are independently selected from this water, find the probability that at least one sample will contain one or more bacterial colonies. (Round your answer to four decimal places.) 1 Correct: Your answer is correct. seenKey 1.000 (b) How many 1 cm3 samples should be selected in order to have a probability of approximately 0.95 of seeing at least one bacterial colony

Answer 1

a) 1 = 100% probability that at least one sample will contain one or more bacterial colonies.

b) 1 sample should be selected in order to have a probability of approximately 0.95 of seeing at least one bacterial colony

Explanation:

To solve this question, we need to understand the poisson and the binomial distributions.

Poisson distribution:

In a Poisson distribution, the probability that X represents the number of successes of a random variable is given by the following formula:

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

In which

x is the number of sucesses

e = 2.71828 is the Euler number

`\mu` is the mean in the given interval.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

Probability of a single sample having at least one bacterial colonies.

Poisson distribution with a mean of 3 per cubic centimeter (cm3), which means that
`\mu = 3`

This is:

`P(X \geq 3) = 1 - P(X = 0)`

In which

`P(X = x) = (e^(-\mu)*\mu^(x))/((x)!)`

`P(X = 0) = (e^(-3)*3^(0))/((0)!) = 0.0495`

`P(X \geq 3) = 1 - P(X = 0) = 1 - 0.0495 = 0.9505`

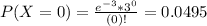
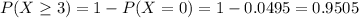
(a) If eight 1 cm3 samples are independently selected from this water, find the probability that at least one sample will contain one or more bacterial colonies.

Multiples samples means that the binomial distribution is used.

0.9505 probability of a sample having at least one colony, which means that
`p = 0.9505`

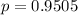
8 samples means that
`n = 8`

The desired probability is:

`P(X \geq 1) = 1 - P(X = 0)`

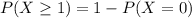
In which

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(8,0).(0.9505)^(0).(0.0495)^(8) \approx 0`

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0 = 1`

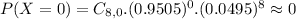
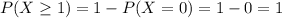
1 = 100% probability that at least one sample will contain one or more bacterial colonies.

(b) How many 1 cm3 samples should be selected in order to have a probability of approximately 0.95 of seeing at least one bacterial colony

We have to find
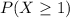`P(X \geq 1)` for samples of 1,2,3,..., until this probability is 0.95. So

n = 1

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(1,0).(0.9505)^(0).(0.0495)^(1) = 0.0495`

`P(X \geq 1) = 1 - P(X = 0) = 1 - 0.0495 = 0.9505`

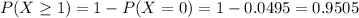
0.9505 > 0.95

1 sample should be selected in order to have a probability of approximately 0.95 of seeing at least one bacterial colony