Answer:
Since the pvalue of 0.0985 > 0.05, we cannot infer that the satisfaction rate is less than the claim with a level of significance of 5%
Explanation:
The null hypothesis is:
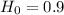
Because tate Farm claims that policyholders have a customer satisfaction rate of greater than 90%.
The alternate hypotesis is:
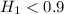
Because of the question: Can we infer that the satisfaction rate is less than the claim with a level of significance of 5%.
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
State Farm claims that policyholders have a customer satisfaction rate of greater than 90%.
This means that
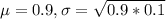
To check the accuracy of this claim, a random sample of 60 State Farm policyholders was asked to rate whether they were satisfied with the quality of customer service.
This means that

Fifteen percent of these policyholders said they were not satisfied with the quality of service.
So 100 - 15 = 85% were satisfied, which means that
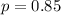
Test statistic:

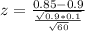
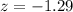
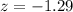 has a pvalue of 0.0985.
has a pvalue of 0.0985.
Since the pvalue of 0.0985 > 0.05, we cannot infer that the satisfaction rate is less than the claim with a level of significance of 5%