Answer:
E(X) = 38.9346
Var(X) = 25.588
E(Y) = 38.25
Var(Y) = 26.1875
Explanation:
Given - Four buses carrying 153 high school students arrive to Montreal. The buses carry, respectively, 36, 46, 32, and 39 students. One of the students is randomly selected.One of the 4 bus drivers is also randomly selected.
To find - Compute the expectations and variances of X and Y.
Proof -
Let us assume that,
X be The number of students that were on the bus carrying this randomly selected student.
Y denote the number of students on his bus.
Now,
E(X) =
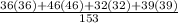
=

= 38.9346
⇒E(X) = 38.9346
Now,
E(Y) =
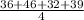
=
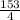
= 38.25
⇒E(Y) = 38.25
Now,
Var(X) =
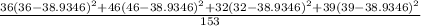
=
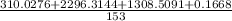
=

= 25.588
⇒Var(X) = 25.588
Now,
Var(Y) = E(Y²) - [E(Y)]²
=
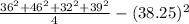
=
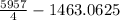
= 1489.25 - 1463.0625
= 26.1875
⇒Var(Y) = 26.1875