Answer:
The 95% confidence interval is (-0.2451, 06912)
Explanation:
From the question, we have;
The number of small cars in the sample of small cars, n₁ = 12
The number of small cars that were totaled, x = 8
The number of large cars in the sample of small cars, n₂ = 15
The number of large cars that were totaled, y = 5
Therefore, the proportion of small cars that were totaled, pX = x/n₁
∴ pX = 8/12 = 2/3
The proportion of large cars that were totaled, pY = y/n₁
∴ pY = 5/15 = 1/3
The 95% confidence interval for the difference pX - pY is given as follows;
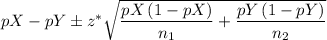
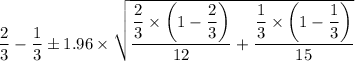
Therefore, we have;
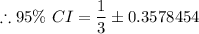
The 95% confidence interval, CI = (-0.2451, 06912)