Answer:
The 99% confidence interval for the fraction of U.S. adult Twitter users who get some news on Twitter is between 49.34% and 60.66%, which means that we are 99% sure that the true percentage of US adult Twitter users who get some news is in this interval.
Explanation:
Confidence interval:
A confidence interval has the following format:
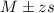
In which M is the sample mean, z is related to the confidence level and s is the standard error.
55% of U.S. adult Twitter users get at least some news on Twitter (Pew, 2013). The standard error for this estimate was 2.2%.
This means that
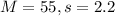
99% confidence level
So
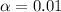 , z is the value of Z that has a pvalue of
, z is the value of Z that has a pvalue of
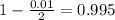 , so
, so
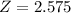 .
.
Lower bound of the interval:

Upper bound:
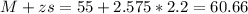
The 99% confidence interval for the fraction of U.S. adult Twitter users who get some news on Twitter is between 49.34% and 60.66%, which means that we are 99% sure that the true percentage of US adult Twitter users who get some news is in this interval.