Answer:
The thickness of the insulator is approximately 34.918 mm
Step-by-step explanation:
From the question, we have;
The outer diameter of the duct, D = 300 mm
The wall thickness of the duct, t₁ = 0.6 mm
The temperature of the inner surface of the duct,
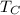 = 0°C
= 0°C
The temperature of the outer surface,
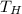 = 25°C
= 25°C
The thermal conductivity of sheet metal, k₁ = 100 W/m-K
The thermal conductivity of insulation, k₂ = 0.04 W/m-K
Assumed rate of heat transfer through the walls of the refrigerator per second, Q = 30 W = 30 J/s
Therefore, we have;
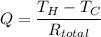
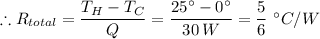
The outside radius, r₂ = 300 mm/2 = 150 mm
The inner diameter of the pipe, d = D - 2·t₁
∴ d = 300 mm - 2 × 0.6 mm = 298.8 mm
The inside radius, r₁ = d/2 = 298.8mm/2 = 149.4 mm
The heat resistance of the pipe, R₁, is given as follows;
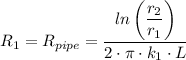
Where;
r₁, r₂, and k₁ are as defined above;
L = The length of the pipe = 1 m
Therefore, we have;
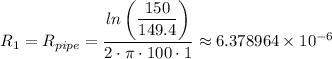
 =
=
 +
+
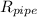
∴
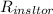 =
=
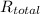 -
-
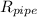
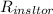 = 5/6 - 6.378964 × 10⁻⁴ ≈ 0.862695
= 5/6 - 6.378964 × 10⁻⁴ ≈ 0.862695
The heat resistance of the insulator, R₂ =
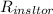 ≈ 0.862695 °C/W
≈ 0.862695 °C/W
The heat resistance of the insulator, R₂, is given as follows;
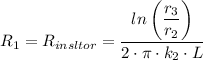
Therefore;
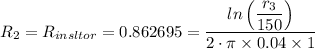
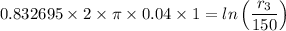
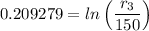
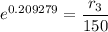
r₃ = 150 ×
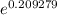 = 184.918
= 184.918
The outer radius of the insulator, r₃ ≈ 184.918 mm
The thickness of the insulator, t₂ = r₃ - r₂
∴ The thickness of the insulator, t₂ ≈ 184.918 mm - 150 mm = 34.918 mm.