Answer:
μ = 0.36
Step-by-step explanation:
This exercise must be solved in parts
Let's start by finding the acceleration of the train, using the kinematics relations
v = v₀ - a t
a =
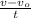
let's reduce the magnitudes to the SI system
v = 66 mi / h (5280 ft / 1mile) (1h / 3600s) = 96.8 ft / s
v₀ = 144 mi / h = 211.2 ft / s
let's calculate
a =
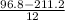
a = - 9.53 ft / s²
Now we can use Newton's second law, for this let's set a reference system with the x axis parallel to the slope of the hill
let's break down the weight
sin 5 = Wₓ / W
cos 5 = W_y / W
Wₓ = W sin 5
W_y = W cos 5
Y axis
N- W_y = 0
N = W cos 5
X axis
Wₓ -fr = m a
mg sin 5 - fr = ma
the friction force has the expression
fr = μ N
fr = μ W cos 5
we substitute
mg sin 5 - μ mg cos 5 = ma
g sin 5 - μ g cos 5 = a
μ =
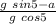
μ =
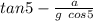
let's calculate
μ = tan 5 - (-9.53) / 32 cos 5
μ = 0.08749 + 0.2733
μ = 0.36