Answer:
Expected value for 4 tickets = $ -7.6
Explanation:
Given - A lottery offers one $900 prize, one $600 Prize, three $400 prizes, and four $100 prizes. One thousand tickets are sold at $5 each.
To find - Find the expectation if a person buys four tickets. Assume that the player's ticket is replaced after each draw and that the same ticket can win more than one prize. Round to two decimal places for currency problems.
Proof -
Given that,
A lottery offers
one $ 900 prize
one $ 600 prize
three $ 400 prizes
Four $ 100 prizes
And
One thousand tickets are sold at $ 5 each
Now,
If the person bought 1000 tickets then the prize he gets is
= 900 + 600 + 3×400 + 4×100
= 900 + 600 + 1200 + 400
= $3100
And
The cost of 1000 tickets = 5×1000 = $ 5000
Now,
Price 1 ticket =
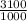 = $ 3.1
= $ 3.1
⇒Expectation of 1 ticket = $ 3.1 - 5 = $ -1.9 (Here $5 is price of 1 ticket)
⇒Expected value for 4 tickets = $ 4× -1.9 = $ -7.6
⇒Expected value for 4 tickets = $ -7.6