Question

In ΔUVW, the measure of ∠W=90°, the measure of ∠U=15°, and VW = 81 feet. Find the length of WU to the nearest tenth of a foot.

Answer 1

The length of WU is 302.3 feet.

Step-by-step explanation:

By Geometry we know that sum of internal angles of a triangle equals 180º, then the measure of angle V is:

`\angle V = 180^(\circ)-\angle U - \angle W` (1)

`\angle V = 180^(\circ)-15^(\circ)-90^(\circ)`

`\angle V = 75^(\circ)`

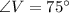
Please notice that segment VW is opposite to angle U and segment WU is opposite to angle V, then we use Law of Sine to calculate the value of the latter segment. All sides are measured in feet:

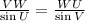`(VW)/(\sin U) = (WU)/(\sin V)` (2)

If we know that
`VW = 81\,ft`,
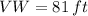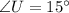`\angle U = 15^(\circ)` and
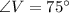`\angle V = 75^(\circ)`, then the length of segment WU is:

`WU = VW \cdot \left((\sin V)/(\sin U) \right)`

`WU = 302.3\,ft`

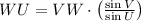
The length of WU is 302.3 feet.