Answer:
The time it would take the element to decay to 28 grams is approximately 22.5 minutes
Explanation:
The give half life of element X = 6 minutes
The given initial mass of the radioactive element X = 390 grams
The mass of the element X after decay = 28 grams
The function that represent the decay of element X is given as follows here;
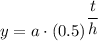
Which is of the form;
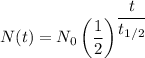
Therefore;
h = 6 minutes = The time duration of the half life
a = N₀ = The initial mass = 390 g
N(t) = The final mass = 28 g
t = The time it takes the element to decay
Plugging in the values gives;
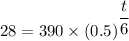

Therefore;

t/6 = ln(29/390)/ln(0.5)
t = 6 × ln(29/390)/ln(0.5) ≈ 22.496
Given the answer to the nearest tenth of a minute, the time it would take the element to decay to 28 grams, t ≈ 22.5 minutes.