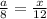Answer:
sin trigonometry ratio
Explanation:
Given
See attachment for triangles
Required
Explain why
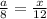
From the attached diagram, both triangles are similar triangles because
(1) the second triangle is a dilation of the first triangle by a ratio of 1.5
i.e
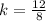
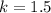
(2) They have angle 30 degrees, and have their right angles located at the same point
In the first triangle, the sine of 30 degrees is represented as:
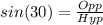
This gives:
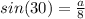
In the second triangle:
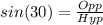
So:

By comparison:

Hence: