Question

A small liberal arts college in the Northeast has 350freshmen. One hundred five of the freshmen are female. Suppose sixty freshmen are randomly selected (without replacement).Step 2 of 2:Find the standard deviation of the number of females in the sample. Round your answer to two decimal places, if necessary.

Answer 1

The standard deviation of the number of females in the sample is 3.21.

Explanation:

For each freshmen, there are only two possible outcomes. Either it is a female, or it is not. Sixty freshmen are randomly selected (without replacement). This means that the hypergeometric distribution is used to solve this question.

Standard deviation of the hypergeometric distribution:

We have that:

N is the population size.

n is the sample size.

s is the number of successes in the sample.

The standard deviation is given by:

`\sigma = \sqrt{n((s)/(N))(1 - (s)/(N))((N - n)/(N-1))}`

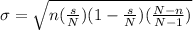
A small liberal arts college in the Northeast has 350freshmen.

This means that
`N = 350`

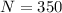
One hundred five of the freshmen are female.

This means that
`s = 105`

Suppose sixty freshmen are randomly selected

This means that
`n = 60`

Find the standard deviation of the number of females in the sample.

`\sigma = \sqrt{60((105)/(350))(1 - (105)/(350))((350 - 60)/(350 -1))} = 3.21`

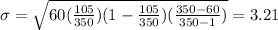
The standard deviation of the number of females in the sample is 3.21.