Question

A 175-kg roller coaster car starts from rest at the top of an 18.0-m hill and rolls down the hill, then up a second hill that has a height of 8.0 m. When the car reaches the top of the second hill, its speed is 11 m/s. Determine the work done by non-conservative forces on the car as it travels from the top of the first hill to the top of the second hill.

Answer 1

The work done by non-conservative forces on the car from the top of the first hill to the top of the second hill is 6574.75 joules.

Step-by-step explanation:

By Principle of Energy Conservation and Work-Energy Theorem we present the equations that describe the situation of the roller coaster car on each top of the hill. Let consider that bottom has a height of zero meters.

From top of the first hill to the bottom

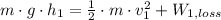`m\cdot g \cdot h_(1) = (1)/(2)\cdot m\cdot v_(1)^(2) +W_(1, loss)` (1)

From the bottom to the top of the second hill

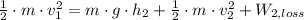`(1)/(2)\cdot m\cdot v_(1)^(2) = m\cdot g \cdot h_(2) + (1)/(2)\cdot m \cdot v_(2)^(2)+W_(2,loss)` (2)

Where:

`m` - Mass of the roller coaster car, in kilograms.

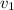`v_(1)` - Speed of the roller coaster car at the bottom between the two hills, in meters per second.

`g` - Gravitational acceleration, in meters per square second.

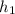`h_(1)` - Height of the first top of the hill with respect to the bottom, in meters.

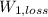`W_(1, loss)` - Work done by non-conservative forces on the car between the top of the first hill and the bottom, in joules.

`v_(2)` - Speed of the roller coaster car at the top of the second hill, in meters per seconds.

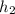`h_(2)` - Height of the second top of the hill with respect to the bottom, in meters.

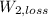`W_(2, loss)` - Work done by non-conservative forces on the car bewteen the bottom between the two hills and the top of the second hill, in joules.

By using (1) and (2), we reduce the system of equation into a sole expression:

`m\cdot g\cdot h_(1) = m\cdot g\cdot h_(2) + (1)/(2)\cdot m \cdot v_(2)^(2) + W_(loss)` (3)

Where
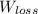`W_(loss)` is the work done by non-conservative forces on the car from the top of the first hill to the top of the second hill, in joules.

If we know that
`m = 175\,kg`,
`g = 9.807\,(m)/(s^(2))`,
`h_(1) = 18\,m`,
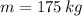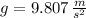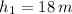`h_(2) = 8\,m` and
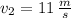`v_(2) = 11\,(m)/(s)`, then the work done by non-conservative force is:

`W_(loss) = m\cdot\left[ g\cdot \left(h_(1)-h_(2)\right)-(1)/(2)\cdot v_(2)^(2) \right]`

`W_(loss) = 6574.75\,J`

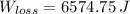
The work done by non-conservative forces on the car from the top of the first hill to the top of the second hill is 6574.75 joules.