Question

Dave sold 60 general and reserved tickets for a concert. He sold general tickets for $10 each and reserved tickets for $15 each collecting a total of $725. Write a system of equations to determine the number of tickets he sold at each price and solve your system of equations?

Answer 1

The system is of equations is:

`\left\{ \begin{array}{ll} 10g+15r=725 & \quad \\ g+r=60 & \quad \end{array} \right.`

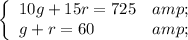
Where g is the amount of general tickets and r is the amount of reserve tickets.

35 general tickets and 25 reserve tickets were sold.

Explanation:

Let general tickets be represented by g and reserved tickets be represented by r.

Each general ticket sells for $10 each and reserved tickets $15 each. Dave collected a total of $725. Thus:

`10g+15r=725`

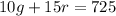
And a total of 60 tickets were sold. Hence:

`g+r=60`

Our system of equations is:

`\left\{ \begin{array}{ll} 10g+15r=725 & \quad \\ g+r=60 & \quad \end{array} \right.`

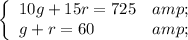
We can solve by substitution. First, divide both sides of the first equation by 5:

`2g+3r=145`

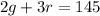
Next, we can subtract a variable (r in this case) from the second equation:

`g=60-r`

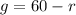
Substitute:

`2(60-r)+3r=145`

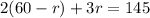
Distribute:

`120-2r+3r=145`

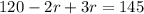
Simplify:

`120+r=145`

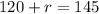
Subtract:

`r=25`

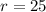
Using the previous equation:

`g=60-r`

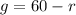
Substitute and evaluate:

`g=60-(25)=35`

So, 35 general tickets and 25 reserve tickets were sold.