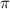Answer:
288
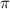
- cone with radius 12 and height 6
- cylinder with diameter 8 and height 18
- sphere with diameter 12
972
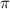
- cone with diameter 18 and height 36
- cylinder with diameter 12 and height 27
- sphere with radius 9
Explanation:


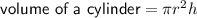

(where r is the radius, h is the height and d is the diameter)
Input the given values of r (d) and/or h into the above equations
Cone
r = 12, h = 6: volume = 288
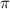
d = 18 ⇒ r = 9, h = 36: volume = 972
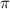
Cylinder
d = 12 ⇒ r = 6, h = 27: volume = 972
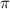
d = 8 ⇒ r = 4, h = 18: volume = 288
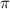
Sphere
d = 12 ⇒ r = 6: volume = 288
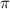
r = 9: volume = 972