Answer:
a) The mean μ = 70.
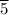
The variance = 127.3203
The standard deviation is 11.28363
b) i) The first quartile is 63.25
ii) The third quartile is 75.5
iii) The 90th percentile is 88.2
Explanation:
a) The city temperatures ae presented as follows;
Fahrenheit; 68, 75, 87, 99, 72, 72, 65, 64, 61, 70, 77, 70, 67, 73, 83, 55, 58, 54
The data points in the sample, N = 18
The mean, μ = ∑
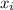 /N
/N
Where;
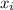 = The value of each data point
= The value of each data point
N = The sample size = 18
From Microsoft Excel, we have;
∑
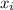 = 1,270
= 1,270
∴ μ = 1,270/18 = 70.
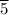
The mean μ is 70.
The variance is given as follows;
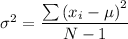
The variance = 127.3203
The standard deviation is given as follows;

We get σ = 11.28363
The standard deviation, σ = 11.28363
b) i) The first quartile, Q₁, is the (n + 1)/4th term
∴ The first quartile is the (18 + 1)/4 = 19/4 = 4.75th term
54, 55, 58, 61, 64, 65, 67, 68, 70, 70, 72, 72, 73, 75, 77, 83, 87, 99
The first quartile = 61 + (64 - 61)×0.75 = 63.25
ii) The third quartile, Q₃, is the 3×(n + 1)/4th term
∴ The third quartile is the 3×(18 + 1)/4 = 57/4 = 14.25th term
Therefore;
Q₃ = 75 + (77 - 75)×0.25 = 75.5
The third quartile is 75.5
iii) The 90th percentile = 90/100 × (18 + 1)th term = 17.1th term
∴ The 90th percentile = 87 + (99 - 87)×0.1 = 88.2