Question

A watermelon is launched from a 25-foot tall platform at a carnival. The watermelon's height h (in feet) at time t seconds can be modeled by the equation h = -16t^2 + 56t + 25. Find the maximum height of the watermelon

Answer 1

The maximum height of the watermelon is 74 feet.

Explanation:

The watermelon reaches its maximum height when its velocity is zero. Mathematically speaking, velocity is the first derivative of the function height, that is:

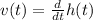`v(t) = (d)/(dt) h(t)` (1)

Where
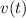`v(t)` is the velocity, in feet per second.

If we know that
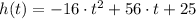`h(t) = -16\cdot t^(2)+56\cdot t +25` and
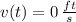`v(t) = 0\,(ft)/(s)`, then the time associated with maximum height is:

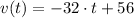`v(t) = -32\cdot t +56` (2)

`-32\cdot t + 56 = 0`

`t = 1.75\,s`

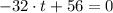
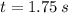
Now we evaluate the function height at time found in the previous step: (
`t = 1.75\,s`)

`h(t) = -16\cdot t^(2)+56\cdot t +25`

`h(1.75) = 74\,ft`

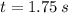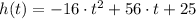
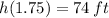
The maximum height of the watermelon is 74 feet.