Question

`\binom{ \sin( \alpha) + \sin( 2alpha ) }{1 + \cos( \alpha ) + \cos(2 \alpha ) } = \tan( \alpha )`

​

Answer 1

I see you use the TeX command "\binom" for binomial coefficient, but I think you meant to use "\frac" to write a fraction, namely,

`(\sin(\alpha)+\sin(2\alpha))/(1+\cos(\alpha)+\cos(2\alpha))=\tan(\alpha)`

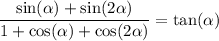
and I assume you're supposed to establish an identity.

Recall the double angle identities for cos and sin :

cos(2α) = cos²(α) - sin²(α) = 2 cos²(α) - 1

sin(2α) = 2 sin(α) cos(α)

Now expand the left side as

(sin(α) + sin(2α)) / (1 + cos(α) + cos(2α)) = (sin(α) + 2 sin(α) cos(α)) / (1 + cos(α) + 2 cos²(α) - 1)

Factor sin(α) from the numerator, and after canceling the 1s in the denominator and factor cos(α) :

… = [sin(α) (1 + 2 cos(α))] / [cos(α) (1 + 2 cos(α))]

Cancel the factors of 1 + 2 cos(α) :

… = sin(α) / cos(α)

which is equivalent to

… = tan(α)

by definition of tan.