Question

When an object is thrown upwards with a speed of 64 ft/sec, its height above the ground is given by the function h(t)=−16t2+64t , where t is the time in seconds after it has been thrown. At what time will the object reach its highest point?

Answer 1

The object will reach its highest point 0.5 seconds after it has been thrown.

Explanation:

The object reaches its maximum height when velocity is equal to zero, the velocity is the derivative of function height. That is:

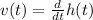`v(t) = (d)/(dt)h(t)` (1)

Where
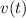`v(t)` is the velocity of the object at time
`t`, in feet per seconds.

If we know that
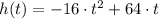`h(t) =-16\cdot t^(2)+64\cdot t` and
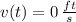`v(t) = 0\,(ft)/(s)`, then the time when object reaches its highest point is:

`v(t) = -32\cdot t+64`

`-32\cdot t + 64 = 0`

`t = 0.5\,s`

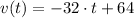
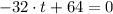
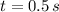
The object will reach its highest point 0.5 seconds after it has been thrown.