Question

18. Find the value of x that makes the equation true.

Answer 1

Explanation:

✧
`\large{ \tt{ \: (1)/(2) x + 2 = (3)/(2) x - 6}}`

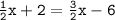
We need to get rid of the fractions. Notice that there are 4 terms in the equation. Multiply both sides of the equation by 2 to get rid of the fractions. Multiply by 2 because 2 is the denominator.

⤑
`\large{ \tt{2( (1)/(2) x + 2) = 2( (3)/(2) x - 6)}}`

⤑
`\large{ \tt{x + 4 = 3x - 12}}`

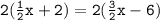
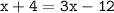
Subtract 4 from both sides in order to isolate the variable on the left.

⤑
`\large{ \tt{x + 4 - 4 = 3x - 12 - 4}}`

⤑
`\large{ \tt{x = 3x - 16}}`

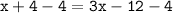
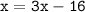
Move 3x to left hand side and change it's sign

⤑
`\large {\tt{x - 3x = - 16}}`

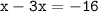
Subtract 3x from 1x

⤑
`\large{ \tt{ - 2x = - 16}}`

Divide both sides of the equation by -2

⤑
`\large{ \tt{ ( - 2x)/( - 2) = ( - 16)/( - 2)}}`

⤑
`\large{ \tt{x = 8}}`

`\boxed{ \boxed{ \underline{ \tt{Our \: Final \: Answer : \boxed{ \underline{ \tt{x = 8}}}}}}}`

Hope I helped ! ♡

Have a wonderful day / night ! ツ

☞
`\underline{ \underline{ \mathfrak{Carry \:On \:Learning}}}`!!▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁▁