Answer:
The increase internal energy is 1,760.41
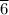 J
J
Step-by-step explanation:
The given parameters of the worker, sledgehammer, and rail line are;
The mass of the spike driven into the rail, m₁ = 0.500 kg
The mass of the sledgehammer, m₂ = 2.50 kg
The speed of the sledgehammer, v = 65.0 m/s
The fraction of the hammers kinetic energy, KE, converted to the internal energy of the hammer and the spike, Δ
 = 1/3 × KE
= 1/3 × KE
Therefore, we have;
The kinetic energy, KE, of the sledgehammer is given by KE = 1/2·m₂·v²
Where;
m₂ = The mass of the sledge hammer = 65.0 m/s
v = The velocity o the sledgehammer
∴ KE = 1/2 × 2.50 kg × (65.0 m/s)² = 5,281.25 J
Therefore;
The increase internal energy, Δ
 = 1/3 × 5,281.25 J = 1760.41
= 1/3 × 5,281.25 J = 1760.41
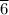 J
J