Answer:
The maximum error in the calculated surface area is approximately 8.3083 square centimeters.
Explanation:
The circumference (
 ), in centimeters, and the surface area (
), in centimeters, and the surface area (
 ), in square centimeters, of a sphere are represented by following formulas:
), in square centimeters, of a sphere are represented by following formulas:
 (1)
(1)
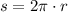 (2)
(2)
Where
 is the radius of the sphere, in centimeters.
is the radius of the sphere, in centimeters.
By applying (2) in (1), we derive this expression:
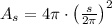
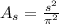 (3)
(3)
By definition of Total Differential, which is equivalent to definition of Linear Approximation in this case, we determine an expression for the maximum error in the calculated surface area (
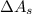 ), in square centimeters:
), in square centimeters:
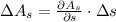
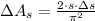 (4)
(4)
Where:
 - Measure circumference, in centimeters.
- Measure circumference, in centimeters.
 - Possible error in circumference, in centimeters.
- Possible error in circumference, in centimeters.
If we know that
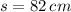 and
and
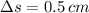 , then the maximum error is:
, then the maximum error is:

The maximum error in the calculated surface area is approximately 8.3083 square centimeters.