Question

In the diagram below of triangle ABC, D is a midpoint of AB and E is a midpoint

of BC. If DE = 4x + 4, and AC = x + 36, what is the measure of DE?
В.
D
E
A
С

Answer 1

DE = 20 units

Explanation:

GIVEN :-

• D & E are the mid-points of AB & BC respectively.
• DE = 4x + 4
• AC = x + 36

TO FIND :-

• Measure of DE

FACTS TO KNOW BEFORE SOLVING :-

• The midsegment of a triangle is a line constructed by connecting the midpoints of any two sides of the triangle.

• The Triangle Midsegment Theorem tells us that a midsegment is one-half the length of the third side (the base), and it is also parallel to the base.

PROCEDURE :-

According to Triangle Midsegment Theorem ,

`DE = (AC)/(2)`

`=> 4x + 4 = (x + 36)/(2)`

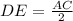
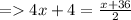
Multiplying 2 on both the sides ,

`=> 2(4x + 4) = x + 36`

`=> 8x + 8 = x + 36`

`=> 8x - x = 36 - 8`

`=> 7x = 28`

`=> x = (28)/(7) = 4`

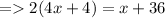
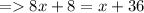
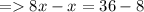
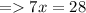
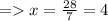
∴ DE = 4×4 + 4 = 20 units