Answer:
The resultant speed = 181.3 mph
The final direction = 38.7° northeast.
Explanation:
We need to find the component in the x-direction and in the y-direction of the speed:
For the plane:
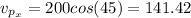
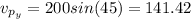
For the wind we have:
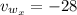
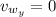
Now, the total speed in the x-direction and in the y-direction is:
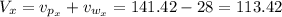
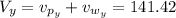
Hence, the resultant speed is:
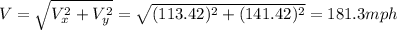
Finally, the direction of the plane is:
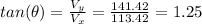

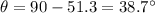
The plane is moving at 38.7° northeast.
I hope it helps you!