Question

What is the equation of the line, in standard form, that passes through (4, -3) and is parallel to the line whose equation is 4x + y - 2 = 0?

4 x + y = 13
4 x + y = -13
4 x - y = 13

Answer 1

Answer:4 x + y = 13 its right trust me

Explanation:

Answer 2

Given:

The equation of parallel line is

`4x+y-2=0`

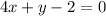
The required line passes through the point (4,-3).

To find:

The equation of required line is standard form.

Solution:

The standard form of a line is

`Ax+By=C`

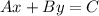
Where, A,B,C are constants and the slope of the line is
`-(A)/(B)`.

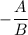The given equation is

`4x+y-2=0`

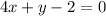
Here,
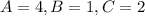`A=4,B=1,C=2`. So, the slope of the line is

`m=-(4)/(1)`

`m=-4`

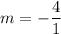
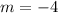
Slopes of parallel lines are equal. So, the slope of the required line is -4

The required line passes trough the point (4,-3) with slope -4. So, the equation of the required line is

`y-y_1=m(x-x_1)`

`y-(-3)=-4(x-4)`

`y+3=-4x+16`

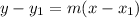
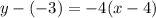
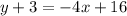
Isolate variable terms.

`4x+y=16-3`

`4x+y=13`

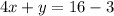
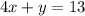
Therefore, the correct option is A.