Question

The volume of a cylinder is represented by the equation V Tarah, where V is the

volume of the cylinder, r is the radius of the base, and h is the height of the cylinder.
Solve the equation in terms of r.

Answer 1

`r=\sqrt{(3V)/(\pi h)}`

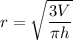
Explanation:

The volume of a cylinder is given by :

`V=(1)/(3)\pi r^2h` .....(1)

Where

r and h are the radius and the height of the cylinder.

We need to solve the equation of r. Cross multiplying both sides in equation (1).

`3V=\pi r^2h`

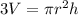
Dividing both sides by
`\pi h`. So,

`(3V)/(\pi h)=(\pi r^2h)/(\pi h)\\\\r^2=(3V)/(\pi h)\\\\or\\\\r=\sqrt{(3V)/(\pi h)}`

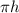So, the radius of the cylinder is equal to
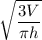`\sqrt{(3V)/(\pi h)}`.