Question

A jar contains 3 orange balls, 3 yellow balls, and 4 red balls. Providing the ball drawn first is replaced before the second is drawn. What is the probability of selecting:

1. 2 orange balls
2. 2 yellow balls
3. 1 red and 1 yellow ball

Answer 1

Given:

Number of orange balls = 3

Number of yellow balls = 3

Number of red balls = 4

To find:

The probability of:

1) 2 orange balls

2) 2 yellow balls

3) 1 red and 1 yellow ball

Solution:

We know that,

`\text{Probability}=\frac{\text{Favorable outcomes}}{\text{Total outcomes}}`

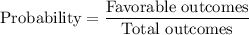
The total number of balls is

`3+3+4=10`

Using the above formula, we get

`P(Orange)=(3)/(10)`

`P(Yellow)=(3)/(10)`

`P(Red)=(4)/(10)`

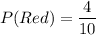
The ball drawn first is replaced before the second is drawn. So, the probabilities remains unchanged.

1) The probability of getting the 2 orange balls is

`P(\text{Orange and orange})=(3)/(10)* (3)/(10)`

`P(\text{Orange and orange})=(9)/(100)`

`P(\text{Orange and orange})=0.09`

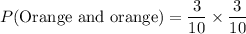
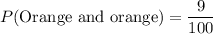
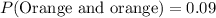
Therefore the probability of getting the 2 orange balls is 0.09.

2) The probability of getting the 2 yellow balls is

`P(\text{yellow and yellow})=(3)/(10)* (3)/(10)`

`P(\text{yellow and yellow})=(9)/(100)`

`P(\text{yellow and yellow})=0.09`

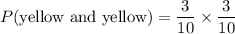
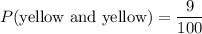
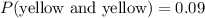
Therefore the probability of getting the 2 yellow balls is 0.09.

3) The probability of getting the 1 red and 1 yellow ball is

`P(\text{Red and yellow})=(4)/(10)* (3)/(10)`

`P(\text{Red and yellow})=(12)/(100)`

`P(\text{Red and yellow})=0.12`

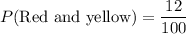
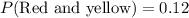
Therefore the probability of getting the 1 red and 1 yellow ball is 0.12.