Question

There are 10 girls and 15 boys in a race. What is the probability that the first, second and third place winners will be boys?

Answer 1

Given:

Number of girls = 10

Number of boys = 15

To find:

The probability that the first, second and third place winners will be boys.

Solution:

Total number of boys and girls:

`10+15=25`

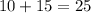
The probability that the first place winner will be a boy is

`P(\text{Boy at first place})=(15)/(25)`

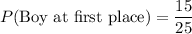
Now, the remaining number of boys is 14. So, the probability that the first place winner will be a boy is

`P(\text{Boy at second place})=(14)/(24)`

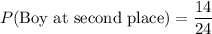
Now, the remaining number of boys is 13. So, the probability that the first place winner will be a boy is

`P(\text{Boy at third place})=(13)/(23)`

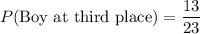
The probability that the first, second and third place winners will be boys is

`P(BBB)=(15)/(25)* (14)/(24)* (13)/(23)`

`P(BBB)=(3)/(5)* (7)/(12)* (13)/(23)`

`P(BBB)=(1)/(5)* (7)/(4)* (13)/(23)`

`P(BBB)=(91)/(460)`

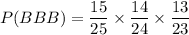
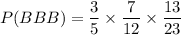
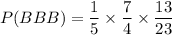
Therefore, the probability that the first, second and third place winners will be boys is
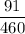`(91)/(460)`.