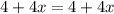Complete Question:
Complete each equation, so the statement about its solution is true.
No solutions:
6-3+4x+1= __x + __
One solution:
6-3+4x+1= __x + __
Infinitely many solutions:
6-3+4x+1 = __x + __
Answer:
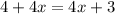 --- No solution
--- No solution
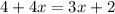 --- One solution
--- One solution
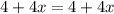 --- Infinitely Many solution
--- Infinitely Many solution
Explanation:
Solving (a): No solutions
6-3+4x+1= __x + __
Collect like terms
6-3+1+4x= __x + __
4+4x= __x + __
To get no solution, the coefficient of x on both sides must be the same. However, the constant must be different.
So, we can equate the expression to:
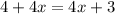
Solving (b): One solution
6-3+4x+1= __x + __
This gives (same as (a))
4+4x= __x + __
To get one solution, the coefficient of x on both sides must be different. The constant can have any value.
So, we can equate the expression to:
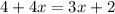
Solving (c): Infinitely many solutions
6-3+4x+1= __x + __
This gives (same as (a))
4+4x= __x + __
To get infinitely many solutions, both sides of the equation must be equal.
So: