Answer:

Explanation:
This is a right triangle, so the trigonometric ratios can be used.
- sinθ= opposite/hypotenuse
- cosθ= adjacent/hypotenuse
- tanθ= opposite/adjacent
Examine the sides. We see that 10 is the hypotenuse (it is opposite the right angle). 6.5 is adjacent to x. So, we should use cosine.
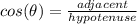

Since we are solving for an angle, we use the inverse trigonometric function.
Move the cosine to the other side and use the inverse.
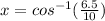
Put the right side into a calculator.
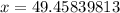
Round to the nearest whole number. The 4 in the tenth place tells us to leave the number as is.
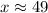
x is approximately 49 degrees.