Answer:
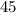
Explanation:
In this case, we take as reference points A and point A'. The point A' is "right under" point P if we draw a line between them. So we can draw another horizontal line that passes through point P that is perpendicular to the line that we first drew. This would give a pair of reference axis to which we will measure the angle of rotation.
Note first that to map point A to point A', we necessarily need to move the triangle in a counterclockwise manner. This, by definition, means that we are doing a rotation by a positive angle. This discards the first two possible options
Now, using the lines that joins the point P and A as reference. We can see that the angle between this line and the black horizontal line and the angle between this line and the black vertical lines is the same. This means that the line PA is splitting the angle between this two lines in exactly the same measure. Since the angle between the black line is 90°, if x is the measure of the angle between line PA and the vertical black line, we would get that:
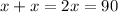
So, dividing both sides by 2, we get;
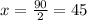
so,The angle of rotation is 45°