Question

Flying to Tahiti with a tailwind a plane averaged 259 km/h. On the return trip the plane only

averaged 211 km/h while flying back into the same wind. Find the speed of the wind and the
speed of the plane in still air.

Answer 1

`\bold{\huge{\underline{ Solution }}}`

Given :-

• Flying to Tahiti with a tailwind a plane averaged speed is 259km/h
• On return trip, The plane only averaged 211km/h with the same wind

To Find :-

• We have to find the speed of the wind and the speed of the plane in still air

Let's Begin :-

Let assume that the speed of plane is x

whereas, The speed of the wind is y

According to the first condition

• Flying to Tahiti with a tailwind a plane averaged speed is 259 km/h

That is,

Speed of plane + Speed of wind = 259 km/h

Subsitute the required variables,

`\bold{ x + y = 259 }`

`\sf{ x = 259 - y...eq(1) }`

According to the second condition

• On the return trip, The plane only averaged speed is 211 km/h with the air

That is,

Speed of plane - Speed of wind = 211 km/h

`\bold{ x - y = 211 ...eq(2) }`

Subsitute eq(1) in eq( 2 ) :-

`\sf{ 259 - y - y = 211 }`

`\sf{ 259 - 2y = 211 }`

`\sf{ - 2y = 211 - 259 }`

`\sf{ - 2y = -48 }`

`\sf{ y = }{\sf{(-48)/(-2)}}`

`\sf{ y = }{\sf{\cancel{(-48)/(-2)}}}`

`\bold{ y = 24 }`

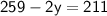
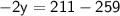
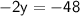
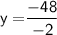
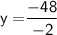
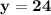
Thus, The speed of wind that is y is 24 km/h

Now,

Subsitute the value of y in eq(1) :-

`\sf{ x = 259 - 24 }`

`\bold{ x = 235 }`

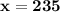
Hence, The speed of the wind and the plane in still is air are 24km/h and 235km/h .

Answer 2

• 235 km/h and 24 km/h

Explanation:

Let the speed of the plane in sill air is p and the speed of the wind is w.

We have the following equations:

• p + w = 259
• p - w = 211

Add up the equations and solve for p:

• 2p = 259 + 211
• 2p = 470
• p = 235

Find the value of w:

• 235 + w = 259
• w = 259 - 235
• w = 24