Answer:
b = 0.938
Explanation:
Value of the car can be modeled by the function,
V(t) =
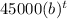
Since, formula for the depreciation is modeled by,
V(t) =
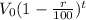
Here, V(t) = Final value of the car after t years
V(0) = Initial value of the car
r = rate of depreciation
t = Time (in years)
By comparing both the functions which are similar,
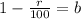

b = 1 - 0.062
b = 0.938