Question

A farmer claims that the average mass of an apple grown in his orchard is 100g. To test this claim, he measures the mass of 150 apples that are grown in his orchard and determines the average mass per apple to be 98g. The results are calculated to be statistically significant at the 0.01 level. What is the correct interpretation of this calculation?

A. The data are not statistically significant at the 0.05 level.
B. The mean mass of any 150 apples grown in the farmer's orchard is 98g.
C. At the 0.01 level of significance, the mean mass of the apples grown in the farmer's orchard is different from 100g.
D. At the 0.01 level of significance, the mean mass of the apples grown in the farmer's orchard is 98g.

Answer 1

C. At the 0.01 level of significance, the mean mass of the apples grown in the farmer's orchard is different from 100g.

Explanation:

The null hypothesis is:

`H_(0) = 100`

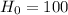
Because of the claim of the farmer.

The alternate hypothesis is:

`H_(1) \\eq 100`

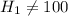
The alternate hypothesis tests the farmer's claim at a significance level.

The results are calculated to be statistically significant at the 0.01 level.

This means that at the 0.01 level, the null hypothesis is rejected, that is, the mean mass of the farmer's orchard is different from 100. Since it is significant at the 0.01 level, it will be significant at the 0.05, 0.1, and increasing levels. So the correct answer is given by option C.