Question

A diver leaves the end of a 5.00 m high diving board and reaches a maximum height of 5.50 m before she strikes the water below. The landing point is 3.25 m beyond the end of the diving board in the horizontal direction. You may approximate the diver as a point particle. Hint: Carefully consider your placement of the origin before starting your calculations.

Determine:_____.
(a) After the diver leaves the diving board, how long does it take for her to strike the water?
(b) The initial velocity of the projectile 7. (hint: a vector has both direction and magnitude).
(c) The final velocity with which the diver enters the water ö, (hint: a vector has both direction and magnitude).

Answer 1

a) 1.38 s

b) v₀ = 3.92 m/s θ₀ = 53.1º

c) vf = 10.7 m/s θf = -77.2º

Step-by-step explanation:

a)

• Once the diver leaves the board, she has an initial velocity vector, that we can split in two directions perpendicular each other, the vertical direction (coincident with the y-axis, positive upward) and the horizontal direction (coincident with the x-axis, positive away from the diving board).
• These velocities, are independent each other, due to they are perpendicular.
• In the horizontal direction, since no acceleration takes place, she keeps the horizontal component v₀ₓ, constant.
• In the vertical direction, she is always accelerated downward by gravity, which constant value is g = 9.8m/s2.
• With this all information, we can find the total time since she left the diving board till she strikes the water below, taking advantage of the fact that she reached to a maximum height of 5.5 m,i.e. , 0.5m above the diving board.
• When at this point, the vertical component of the velocity is zero, so we can write the following kinematic equation:

`v_(fy) ^(2) - v_(oy) ^(2) = 2* g* \Delta y (1)`

• Solving for v₀y in (1):

`v_(oy) = \sqrt{2*g*\Delta_(ymax) } = √(2*9.8m/s2*0.5m) = 3.13 m/s (2)`

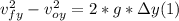
• When she is at the highest point, her final vertical speed is zero, so we can find the time when she reached to this point, applying the definition of acceleration, as follows:

`v_(fyhmax) = v_(oy) - g*t_(hmax) = 0 (3)`

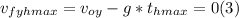
• Solving for t in (3), we get:

`t_(hmax) =- (v_(oy))/(g) =(3.13m/s)/(9.8m/s2) = 0.32 s (4)`

• Since at this point, the vertical speed is zero, we can apply the equation for the displacement (vertical in this case) for a total displacement of 5.5 m (taking as the origin the point just below the end of the diving board, on the surface of the water), with initial speed equal to zero, as follows:

`\Delta y = (1)/(2)* g * t^(2) = 5.5 m (5)`

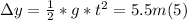
• Solving for t (which we will call t₂) in (5), we get:

`t_(2) = \sqrt{(2*\Delta y)/(g)} = \sqrt{(2*5.5m)/(9.8m/s2) } = 1.06 s (6)`

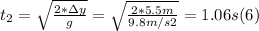
• The total time will be just the sum of (4) (since leaving the diving board till reaching the maximum height) and (6) (from there until she strikes the water), as follows:
• Δt = thmax + t₂ = 0.32 s + 1.06 s = 1.38 s (7)

b)

• In order to know the value of v₀, we need first to get the values of vox and voy.
• We know that the horizontal speed remains constant, so, if we know the total time traveled (same as in a)) and the horizontal distance (given), we can find v₀ₓ applying the definition of average velocity, as follows:

`v_(ox) =(\Delta x)/(\Delta t) =(3.25m)/(1.38s) = 2.36 m/s (8)`

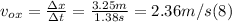
• We know the value of v₀y from (2):

`v_(oy) = 3.13 m/s (9)`

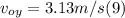
• Applying the Pythagorean theorem, we can get the magnitude of v₀ as follows:

`v_(o) = \sqrt{v_(ox)^(2) + v_(oy)^(2)} = \sqrt{(2.36m/s)^(2) + (3.13m/s)^(2)} = 3.92m/s (10)`

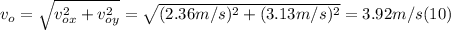
• We can find the angle that it makes with the horizontal, applying the definition of tangent of an angle, as follows:

`tg_((\theta o)) = (v_(oy))/(v_(ox) ) = (3.13)/(2.36) = 1.33 (11)`

⇒ θ₀ = tg⁻¹ (1.33) = 53.1º

c)

• In order to find the vertical component of the final velocity, we can use the following kinematic equation, for the total vertical displacement of 5.5 m since it started to fall after reaching to the maximum speed:

`v_(fy) ^(2) - v_(oy) ^(2) = 2* g* \Delta y (12)`

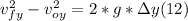
• When it started to fall, in the vertical direction, the diver was at rest, so in (12) we have v₀y = 0.
• Solving for vfy in (12) we get:

`v_(fy) = \sqrt{2*g*\Delta_(y) } = √(2*9.8m/s2*5.5m) = -10.4 m/s (13)`

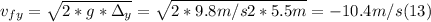
• We already know that the horizontal component is the same as the initial v₀ₓ, so we can find the magnitude of the final velocity applying the Pythagorean Theorem as follows:

`v_(f) = \sqrt{v_(fx)^(2) + v_(fy)^(2)} = \sqrt{(2.36m/s)^(2) + (-10.4m/s)^(2)} = 10.7 m/s (14)`

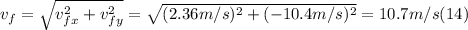
• Finally, as we did in (11) to find the angle that it makes with the horizontal, we can find θf as follows:

`tg_((\theta f)) = (v_(fy))/(v_(fx) ) = (-10.4)/(2.36) = -4.41 (15)`

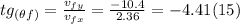
⇒ θf = tg⁻¹ (-4.41) = -77.2º