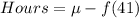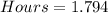Question:
In New York City at the spring equinox there are 12 hours 8 minutes of daylight. The longest and the shortest days of the year vary by 2 hours 53 minutes from the equinox. In this year, the equinox falls on March 21. In this task, you'll use a trigonometric function to model the hours of daylight hours on certain days of the year in New York City.
- Find amplitude and the period of the function
- Create a trigonometric function that describes the hours of sunlight for each day of the year
- Then use the function you built to find how fewer daylight hours February 10 will have then March 21
Answer:
(a)
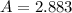 --- Amplitude
--- Amplitude
 ---- Period
---- Period
(b) Trigonometry function
![f(x) = 12.133 + 2.883sin((2\pi)/(365)[x - 80])](https://img.qammunity.org/2022/formulas/mathematics/high-school/v22qeoosz1slcjpfy2g91tjddsz8y70aa8.png)
(c)
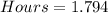
Explanation:
Given


Solving (a): Amplitude (P) and Period (T)
The amplitude is the amount of time the longest and the shortest day vary.
So
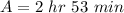
Convert to hours


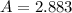
The period (T) is the duration i.e 1 year
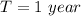
Assume no leap year

Solving (b): Trigonometry function
The function follows a sinusoidal pattern and the general form is:
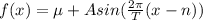
Where
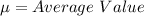
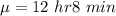
Convert to hours
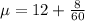
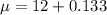
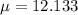
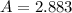 --- Amplitude
--- Amplitude
 ---- Period
---- Period
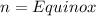
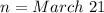
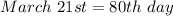
So:

The function becomes:
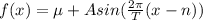
![f(x) = 12.133 + 2.883sin((2\pi)/(365)[x - 80])](https://img.qammunity.org/2022/formulas/mathematics/high-school/v22qeoosz1slcjpfy2g91tjddsz8y70aa8.png)
Solving (c): Fewer daylight hours will Feb. 10 have.
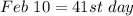
So:
![f(x) = 12.133 + 2.883sin((2\pi)/(365)[x - 80])](https://img.qammunity.org/2022/formulas/mathematics/high-school/v22qeoosz1slcjpfy2g91tjddsz8y70aa8.png)
![f(41) = 12.133 + 2.883sin((2\pi)/(365)[41 - 80])](https://img.qammunity.org/2022/formulas/mathematics/high-school/wgo2gqzb56nd5xsufpwcwmllo18q1gqrp4.png)
![f(41) = 12.133 + 2.883sin((2\pi)/(365)[-39])](https://img.qammunity.org/2022/formulas/mathematics/high-school/jvzre2gu8yi25k9taamv1xxk47f2enb3qx.png)
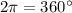
So:
![f(41) = 12.133 + 2.883sin((360)/(365)[-39])](https://img.qammunity.org/2022/formulas/mathematics/high-school/ts2yu0saw6f3ovi12d1lqqn1rgd46a2ywx.png)
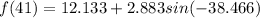
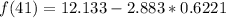
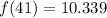
The fewer daylight hours is the calculated as: